深度学习理论

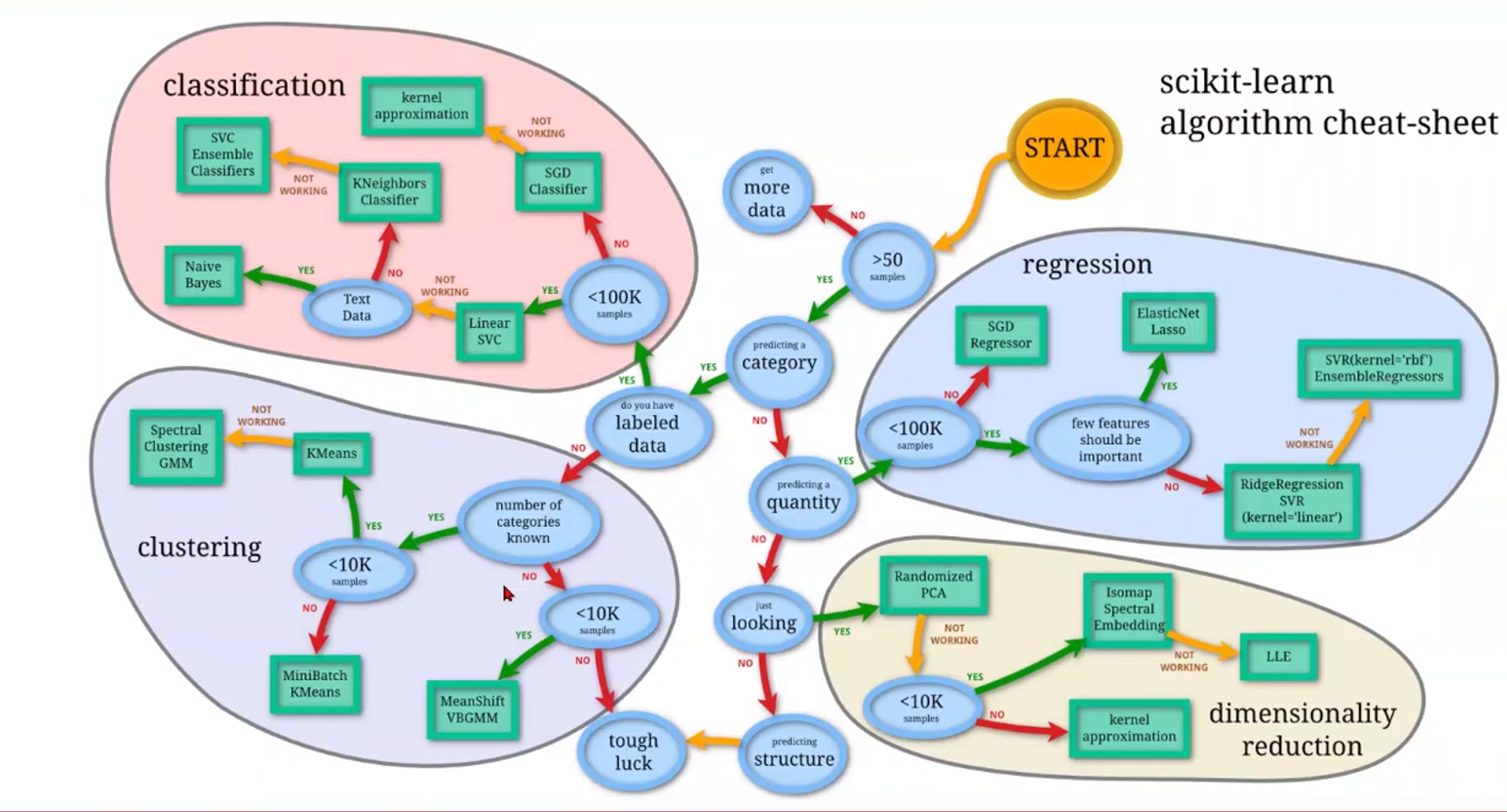
这篇文章讲述深度学习理论知识图谱，包括分类、聚类、回归和降维

深度学习方法概述：分类、聚类、回归和降维

使用Pytorch构建DeepLearning算法的基本流程：

以线性模型为例：

1. DataSet - 数据集准备

2. Model - 模型选择

$$y = w \times x + b$$

3. Training - 训练模型

• 随机初始化 $w$（通常也包含 $b$）
• 定义优化器（如梯度下降）
• 定义损失函数（Loss Function）： $$\text{Loss}^{(i)} = (y_{\text{hat}}^{(i)} - y^{(i)})^2$$
• 优化权重：
  通过改变 $w$ 最小化代价函数（Cost Function）： $$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_{\text{hat}}^{(i)} - y^{(i)})^2$$ （示例方法：穷举所有权重值对应的 MSE）

4. Inferring - 预测应用

确定最优权重 $w$ 后，将模型用于推理/预测：

$$y_{\text{pred}} = w_{\text{final}} \times x_{\text{new}} + b$$

损失函数、目标函数、价值函数概念

• 损失函数 (Loss Function)：单个样本的损失
  $\text{Loss}^{(i)} = f(y_{\text{pred}}^{(i)}, y_{\text{true}}^{(i)})$

• 价值函数 (Value Function)：所有样本损失和的平均值
  $J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \text{Loss}^{(i)}$

• 目标函数 (Objective Function)：需要最小化或最大化的整体函数
  $\min_{\theta} J(\theta) \quad \text{或} \quad \max_{\theta} J(\theta)$

权重W初始化策略

Q：初始化权重值过小会怎样？

答：梯度值下降会非常缓慢

Q：初始化权重值过大会怎样？

答：会导致梯度下降过快，错过最优解

Q：初始化所有权重值W=0会怎样？

答：会导致所有神经元都相同

Q：正确的权重初始化策略有哪些？

1. 初始化w=小的随机数，适用于小型网络

   • 假设：使用 $W = 1 \times \text{np.random.randn}(D,H)$，tanh激活函数会出现什么情况？
     答：网络饱和。权重 $W$ 较大 → 输出较大 → tanh 输出接近 $\pm 1$

2. w从标准高斯分布中取样，依据输入数据数量进行缩放
   $W \sim \mathcal{N}(0, \sigma^2), \quad \sigma = \frac{1}{\sqrt{n_{\text{input}}}}$

优化算法

梯度下降 (GD)

• 特点：性能低，时间复杂度低
• 计算：价值函数的梯度
• 下降方向：负梯度方向
• 步长大小：学习率
• 更新规则：
  $\theta_{t+1} = \theta_t - \eta \nabla J(\theta_t)$
• 优点：可并行计算，凸函数全局最优
• 缺点：无法解决鞍点问题

随机梯度下降 (SGD)

• 特点：性能高，时间复杂度高
• 计算：随机样本的损失函数梯度
• 下降方向：随机选某个样本的损失函数**的负梯度为下降方向更新权重
• 更新规则：
  $\theta_{t+1} = \theta_t - \eta \nabla \text{Loss}^{(i)}(\theta_t)$
• 问题：山谷震荡、鞍点问题，无法并行

Mini-batch 梯度下降

• 方法：将样本分组，计算组内样本损失和的梯度
  $\theta_{t+1} = \theta_t - \eta \nabla \left( \frac{1}{b} \sum_{i=1}^{b} \text{Loss}^{(i)}(\theta_t) \right)$

动量方法 (Momentum)

• 原理：随机梯度下降 + 惯性
• 下降方向：带衰减的前一次的下降方向 + 学习率 * 当前算出的梯度
• 更新规则：($\gamma$: 动量衰减系数) $$\begin{aligned} v_t &= \gamma v_{t-1} + \eta \nabla \theta_t \\ \theta_{t+1} &= \theta_t - v_t \end{aligned}$$

Adagrad

• 原理：随机梯度下降 + 自适应学习率
• 下降方向：（学习率/sqrt(历史梯度的平方和)）* 当前计算出的梯度
• 更新规则： $$\begin{aligned} g_t &= \nabla \theta_t \\ G_t &= G_{t-1} + g_t^2 \\ \theta_{t+1} &= \theta_t - \frac{\eta}{\sqrt{G_t + \epsilon}} \odot g_t \end{aligned}$$
• 缺陷：梯度平方项$G_t$ 单调增 → 学习率 $\downarrow$

Adam

• 原理：随机梯度 + 惯性 + 自适应学习率
• 下降方向：学习率/sqrt(过往梯度平方和当前梯度平方的平均值) * 过往梯度与当前梯度的平均值
• 更新规则： $$\begin{aligned} m_t &= \beta_1 m_{t-1} + (1-\beta_1)g_t \quad &\text{(一阶矩估计)} \\ v_t &= \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \quad &\text{(二阶矩估计)} \\ \hat{m}_t &= \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t} \\ \theta_{t+1} &= \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \end{aligned}$$

手推前馈运算和反向传播

基本步骤

1. 绘制计算图：构建网络计算流程图
2. 前馈计算：计算得到损失函数值 $$\text{Loss} = f(\text{forward}(x, W))$$
3. 计算局部偏导数：基于计算图计算各节点偏导
4. 链式法则：组合局部偏导得到最终梯度 $$\frac{\partial \text{Loss}}{\partial W} = \prod \frac{\partial \text{node}_i}{\partial \text{node}_{i-1}}$$

节点梯度传播规则

加法节点

• 前向传播：$z = x + y$
• 反向传播：梯度直接赋值给所有输入分支 $$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial z}, \quad \frac{\partial L}{\partial y} = \frac{\partial L}{\partial z}$$

Max节点

• 前向传播：$z = \max(x, y)$
• 反向传播：梯度仅回传给最大值分支 $$\frac{\partial L}{\partial x} = \begin{cases} \frac{\partial L}{\partial z} & \text{if } x > y \\ 0 & \text{otherwise} \end{cases}, \quad \frac{\partial L}{\partial y} = \begin{cases} \frac{\partial L}{\partial z} & \text{if } y > x \\ 0 & \text{otherwise} \end{cases}$$
• 解释：前向传播中只有最大值向后传递

倍乘节点

• 前向传播：$z = k \times x$（$k$为常数）
• 反向传播：梯度值按比例缩放 $$\frac{\partial L}{\partial x} = k \times \frac{\partial L}{\partial z}$$

分支节点（一个节点连接多个下游）

• 前向传播：$y_1 = f(x), y_2 = g(x)$
• 反向传播：下游梯度相加回传 $$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y_1} \frac{\partial y_1}{\partial x} + \frac{\partial L}{\partial y_2} \frac{\partial y_2}{\partial x}$$

回归问题与分类问题的联系（以逻辑回归到二分类为例）

在模型外套用激活函数将回归的预测值映射为 (0,1) 之间的概率值，设置分类阈值（通常为 0.5）：

• 预测概率 > 阈值 → 判定为类别 1
• 预测概率 < 阈值 → 判定为类别 0

$$p(y=1|x) = \sigma(w^Tx + b) = \frac{1}{1 + e^{-(w^Tx + b)}}$$

机器学习的本质

学习数据分布：

• 预测值服从一个概率分布 $P_{\text{pred}}(y|x)$
• 真实标签服从一个概率分布 $P_{\text{true}}(y|x)$
• 利用分布之间的差异（如 KL 散度）作为损失函数： $$\mathcal{L} = D_{\text{KL}}(P_{\text{true}} \| P_{\text{pred}})$$
• 计算梯度并更新权重以最小化分布差异

常见激活函数

Sigmoid

公式：

$$\sigma(z) = \frac{1}{1 + e^{-z}}$$

优缺点：

• ✅ 输出范围 (0,1)，适合概率输出
• ❌ 当 $|z|$ 很大时梯度趋于 0（梯度消失）
• ❌ 输出不以 0 为中心（导致梯度恒正/恒负）
• ❌ 指数计算代价高

Tanh

公式：

$$\tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$$

优缺点：

• ✅ 输出范围 (-1,1)，以 0 为中心
• ❌ 当 $|z|$ 很大时梯度趋于 0（梯度消失）
• ❌ 指数计算代价高

ReLU (Rectified Linear Unit)

公式：

$$\text{ReLU}(z) = \max(0, z)$$

优缺点：

• ✅ 计算复杂度低（无指数运算）
• ✅ 解决正区间的梯度消失问题
• ✅ 提供稀疏表达能力（单侧抑制）
• ❌ $z < 0$ 时梯度为 0（神经元死亡问题）

ReLU 改进方案

Leaky ReLU (LReLU)

公式：

$$\text{LReLU}(z) = \begin{cases} z & \text{if } z > 0 \\ \alpha z & \text{if } z \leq 0 \end{cases} \quad (\alpha \approx 0.01)$$

• 使用斜率为 $\alpha$ 的线性函数替代 0
• 缓解神经元死亡问题

ELU (Exponential Linear Unit)

公式：

$$\text{ELU}(z) = \begin{cases} z & \text{if } z > 0 \\ \alpha(e^z - 1) & \text{if } z \leq 0 \end{cases}$$

• 建立负饱和机制
• 对噪声有更好的鲁棒性

Maxout

公式：

$$\text{Maxout}(z) = \max(w_1^Tx + b_1, w_2^Tx + b_2)$$

• 将参数数量翻倍
• 训练两个权重组合，取最大值作为输出
• 能拟合任意凸函数